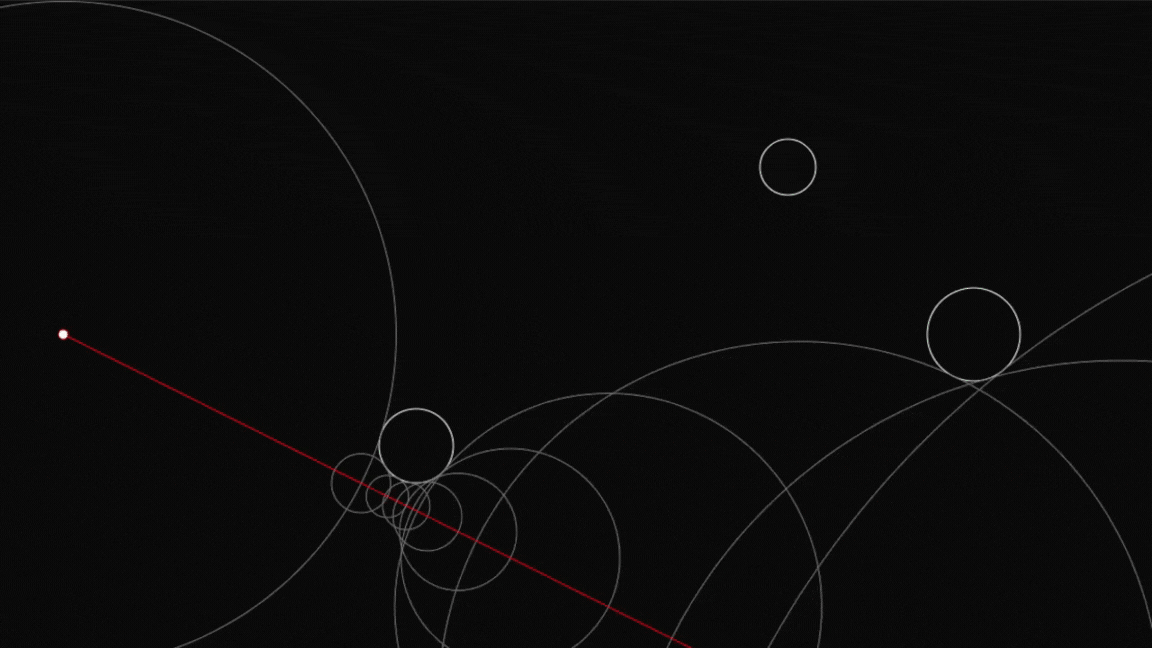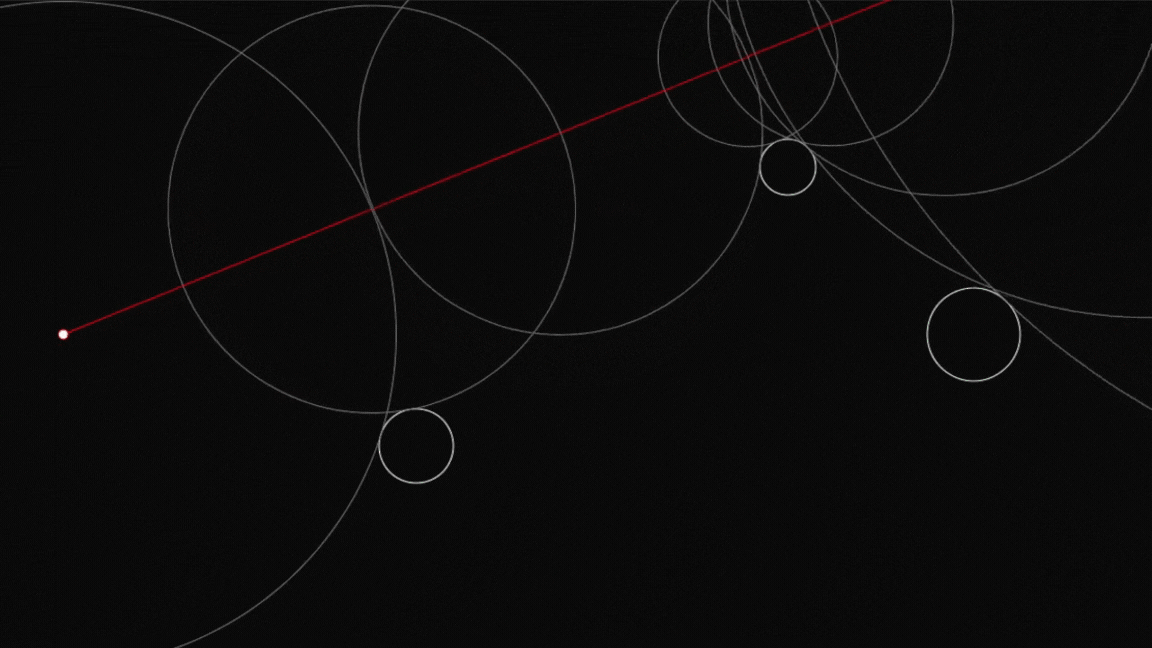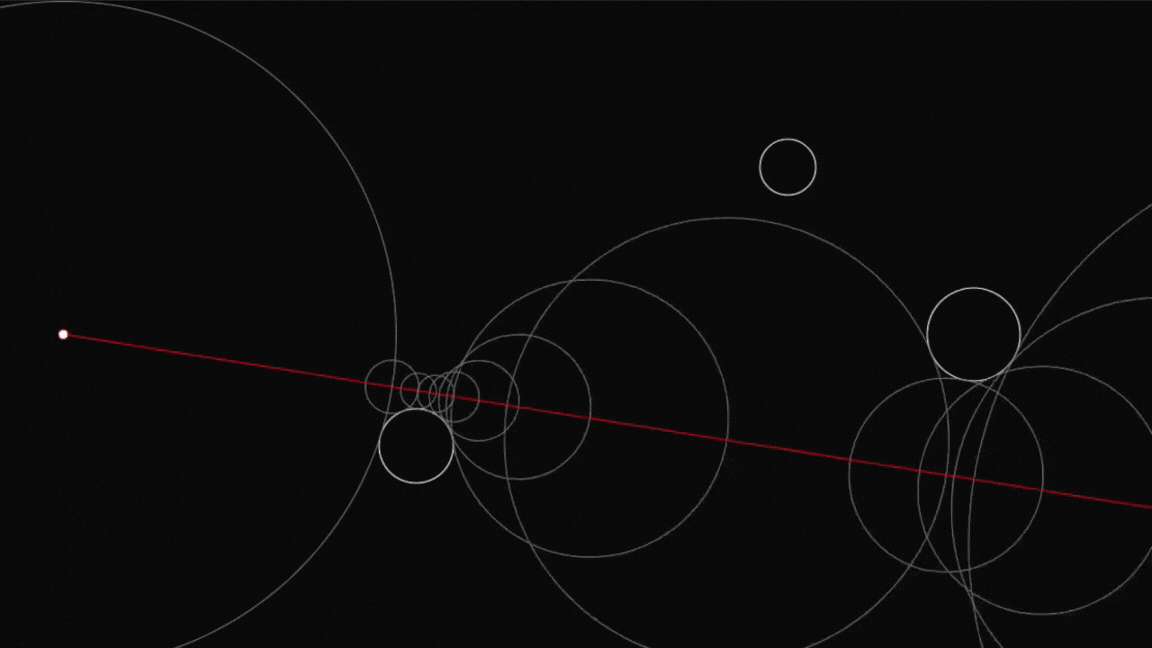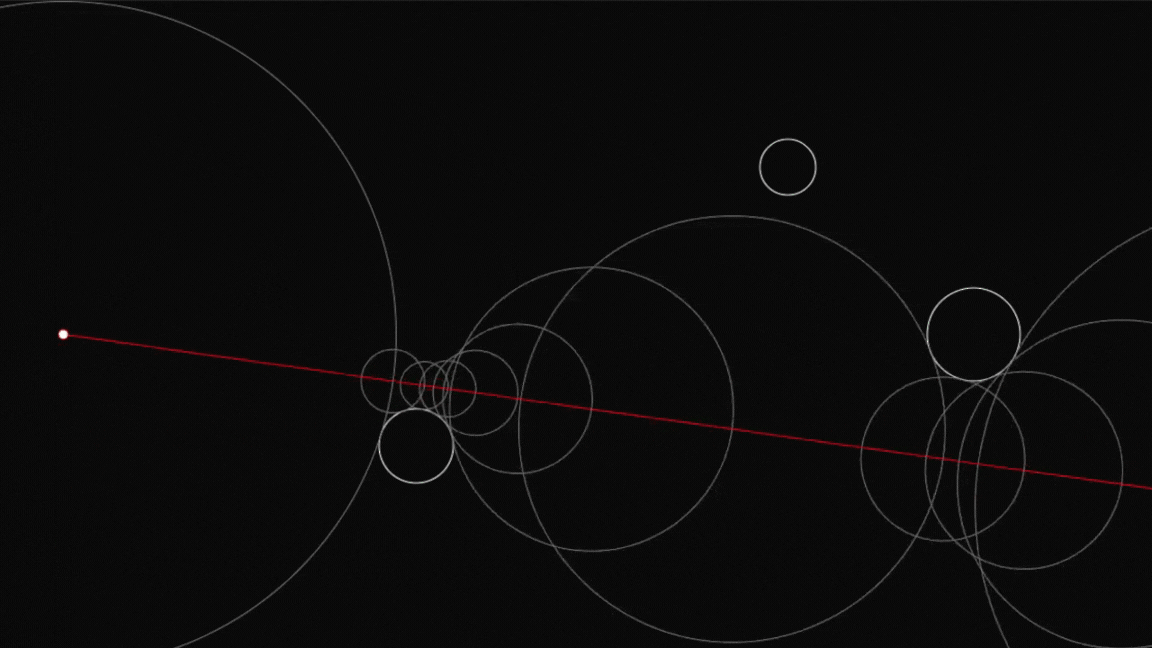
This project implements a real-time 3D Mandelbulb fractal renderer using ray marching. The rendering is done on the GPU via a fragment shader for optimal performance. Over time, the Mandelbulb’s power starts at 0 and gradually increases, creating an evolving fractal effect.

Ray marching is an iterative technique for rendering implicit surfaces. The core of the algorithm involves marching a ray through space and stopping when it gets close to a surface defined by a Signed Distance Function (SDF). The Mandelbulb’s SDF determines the fractal structure.

vec3 rayDirection = normalize(pixelPosition - cameraPosition);
float totalDistance = 0.0;
for (int i = 0; i < MAX_STEPS; i++) {
    vec3 currentPos = rayOrigin + totalDistance * rayDirection;
    float distance = mandelbulb(currentPos, rotationMatrix);
    if (distance < EPSILON) {
        return computeColor(currentPos);
    }
    totalDistance += distance;
    if (totalDistance > MAX_DISTANCE) break;
}
return backgroundColor;

The following demonstrates a 2D version of the ray marching algorithm, helping to visualize how the technique works:

The core function used to determine the Mandelbulb’s shape is an SDF. This function calculates the approximate distance from a given point to the fractal’s surface. The following GLSL code implements the SDF for the Mandelbulb:

float mandelbulb(vec3 p, mat3 rotation) {
    p = rotation * p;  // Apply rotation to the input point

    vec3 z = p;
    float dr = 1.0;
    float r = 0.0;
    float Power = ((time / 1000.0) * 0.1) + 1.0;  // Mandelbulb power increases over time

    for (int i = 0; i < 8; i++) {
        r = length(z);
        if (r > 2.0) break;

        // Convert to polar coordinates
        float theta = acos(z.z / r);
        float phi = atan(z.y, z.x);
        dr =  pow(r, Power - 1.0) * Power * dr + 1.0;

        // Scale and rotate the point
        float zr = pow(r, Power);
        theta = theta * Power;
        phi = phi * Power;

        // Convert back to cartesian coordinates
        z = zr * vec3(sin(theta) * cos(phi), sin(phi) * sin(theta), cos(theta));
        z += p;
    }
    return 0.5 * log(r) * r / dr;
}

This implementation is based on Inigo Quilez’s Mandelbulb SDF: iquilezles.org/articles/mandelbulb/.

To compile and run this project, you need:

• GLFW: A library for OpenGL context creation and handling window events.
• OpenGL: The rendering API used to compute and display the Mandelbulb.

• Real-time rendering: Uses ray marching on the GPU for high performance.
• Dynamic Mandelbulb evolution: The fractal’s power starts at 0 and gradually increases over time.

Ensure you have GLFW installed. If not, you can install it via:

sudo apt-get install libglfw3-dev

brew install glfw

Download and set up GLFW from glfw.org.

g++ -o mandelbulb main.cpp -lglfw -lGL -lGLEW
./mandelbulb

You can download the latest release here.